Решение фундаментальных проблем квантовой теории молекул

1) Рассмотрен важный для понимания базовых основ квантовой химии и теории спектров вопрос о соотношении так называемых полуэмпирических и ab initio формулировок чисто электронной задачи и методов ее решения.
Это имеет принципиальное значение в связи с широким распространением высоко-сервисных программ для ПК, которыми очень большое число исследователей пользуются как «черными ящиками».
Показано, что полуэмпирические и ab initio подходы и методы не являются взаимно исключающими, но, наоборот, взаимодополняют друг друга в полном согласии с принципом дополнительности Н. Бора, и что наиболее рациональный путь дальнейшего развития квантовой химии заключается в поиске «золотой середины».

2) На основании первых принципов предложено квантово-механическое обоснование метода атом–атомных потенциалов, широко применяемого для определения пространственного строения сложных молекулярных систем и молекулярных кристаллов. Показано, что соответствующий подход естественным образом формируется, если обратиться к матричному описанию квантовых проблем и проанализировать физический смысл соответствующих матричных элементов.

3) Уточнено понятие адиабатического приближения и показано, что обычно употребляемое выражение для собственной функции в форме произведения электронной и колебательной составляющих отвечает решению уравнения Шредингера только для одного электронного состояния (терма) и в общем случае не является даже приближенным для электронно-колебательного оператора.

4) Решена ранее не рассматривавшаяся задача о вычислении матричного элемента для дипольного перехода между электронно-колебательными уровнями энергии при сильном изменении положения и характеристик комбинирующихся потенциальных функций. Учтены герцберг-теллеровские члены первого и второго порядков и предложены расчетные формулы, пригодные для работы с реальными многоатомными молекулами.

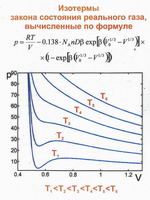
5) Известно, что свойства молекул в конденсированных средах (плотные газы, жидкости) существенно зависят от межмолекулярных взаимодействий. Оценка соответствующих потенциалов представляет большие трудности. Экспериментально межмолекулярные взаимодействия проявляются в двух совокупностях фактов: микроскопических, основанных на измерении ИК спектров возмущенных молекул, и макроскопических, по виду изотермы реального газа при конденсации. Ранее отсутствовала пригодная для конкретных оценок теоретическая связь между характеристиками межмолекулярных потенциалов, определяемыми средствами квантовой химии, и макроповедением всего ансамбля молекул. Впервые сделана попытка установить такую связь, опираясь на наглядную модель.
Для изотерм реального газа получено уравнение, по форме сильно отличающееся от уравнения Ван-дер-Ваальса, но, тем не менее, вполне адекватно описывающее вид изотерм реального газа. Определяемые квантовыми расчётами микрохарактеристики межмолекулярных потенциалов явно входят в уравнение как параметры.

6) Изучение изомерных превращений в органических молекулах требует весьма гибкой системы естественных колебательных координат для описания механических движений, приводящих к изомеризации. В связи с этим возникает совершенно новая задача для теории колебаний молекул, связанная с необходимостью замены в имеющейся модели молекулы части колебательных координат на адекватные задаче об изомеризации с соответствующей корректировкой системы силовых постоянных без изменений частот и смещений атомов при колебаниях.
Разработана специальная методика, осуществляющая это преобразование в автоматическом режиме и исключающая необходимость решения обратных спектральных задач. Разработанный метод и его алгоритмическое обеспечение апробированы на примере модельных расчетов сложных молекул, показавших их высокую эффективность.

7) Дано исчерпывающее доказательство теоремы «линеаризации» произведения приведённых функций Бесселя (ПФБ).
Широкий класс базисных функций в виде ПФБ включает в себя не только все известные типы орбиталей экспоненциального вида, но и функции с экспоненциальной асимптотикой, что позволяет применить развитую методику к разнообразным физико-химическим задачам. Особенно следует подчеркнуть, что данные алгоритмы разрешают проблему вычисления молекулярных структур с тяжелыми элементами Периодической системы элементов Д.И. Менделеева. С помощью интегралов электронных формфакторов удается исследовать структуру решения уравнений Хартри-Фока для молекулы. Для этой цели рассматриваются итерации молекулярных орбиталей с помощью интегральных уравнений Хартри-Фока.
Показано, что расширение первоначального базисного ряда МО ЛКАО при итерациях происходит за счет функций (атомных орбиталей) экспоненциального вида с удвоенными и далее увеличивающимися параметрами Слэтера, что приводит к заполнению внутримолекулярного пространства между ядрами атомов базисными элементами с центрами сначала вдоль отрезков прямых, соединяющих ядра, а при последующих итерациях с центрами во всем пространстве ядерного полиэдра. Таким образом, поляризационные базисные элементы улучшают описание внутримолекулярной электронной плотности, что проверено практикой квантовохимических вычислений, основывающейся на интуитивном представлении физической природы электронного распределения внутри молекулы.

8) Впервые дано математическое обоснование метода построения МО ЛКАО.
Априори не очевидно, что потенциалу притяжения электрона к ядрам молекулы в виде суммы кулоновских потенциалов будет соответствовать решение уравнения Шредингера также в виде линейной комбинации атомных орбиталей. Однако исследование одноэлектронного интегрального уравнения Шредингера в импульсном представлении приводит к структуре решения уравнения Шредингера в виде МО ЛКАО. Этот результат дает теоретическую основу метода МО ЛКАО в квантовой химии.
Аналогичное исследование уравнения Шредингера с потенциалом в виде суммы потенциалов Юкавы приводит также к методу построения решения в виде МО ЛКАО. Атомные орбитали вычисляются как разложения по водородоподобным функциям.
Предложены алгоритмы вычисления соответствующих матричных элементов и проведены тестовые расчеты ряда многоцентровых квантовохимических интегралов, показывающие эффективность разработанных методов.

См. также: Результаты 2003-2006 гг